Deploying new Azure Container Apps with familiar languages
Use the Pulumi Azure Native Provider to deploy containerized apps to Microsoft's new Azure Container Apps platform for serverless apps.
Read more...
Choosing the Number of Shards in Temporal History Service
Tuning the sharding configuration for the optimal cluster performance with the numHistoryShards config.
Read more...
Maru: Load Testing Tool for Temporal Workflows
Benchmarking Temporal deployments with a simple load simulator tool
Read more...
Cold Starts in Serverless Functions
Exploring the phenomenon of increased latency while instances of cloud functions are dynamically allocated.
Read more...
Farmer or Pulumi? Why not both!
Azure Infrastucture as Code using F#: combining Pulumi and Farmer
Read more...
Get Up and Running with Azure Synapse and Pulumi
Use infrastructure as code to automate deployment of an Azure Synapse workspace
Read more...
Running Container Images in AWS Lambda
AWS Lambda launches support for packaging and deploying functions as container images
Read more...
How To Deploy Temporal to Azure Kubernetes Service (AKS)
Get up and running with Temporal workflows in Azure and Kubernetes in several CLI commands
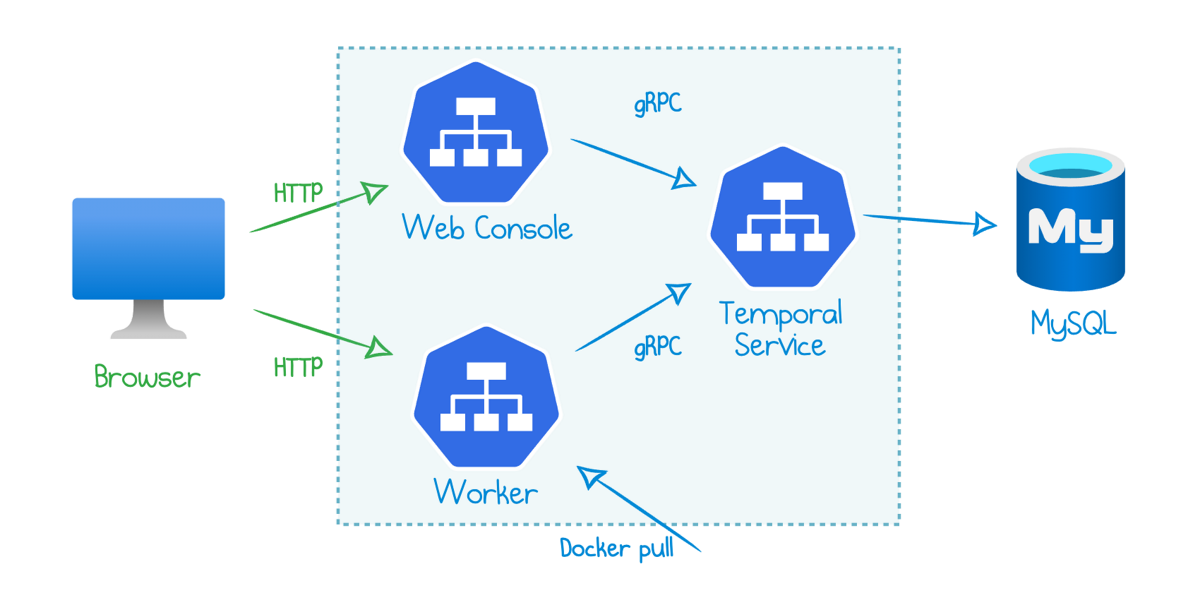
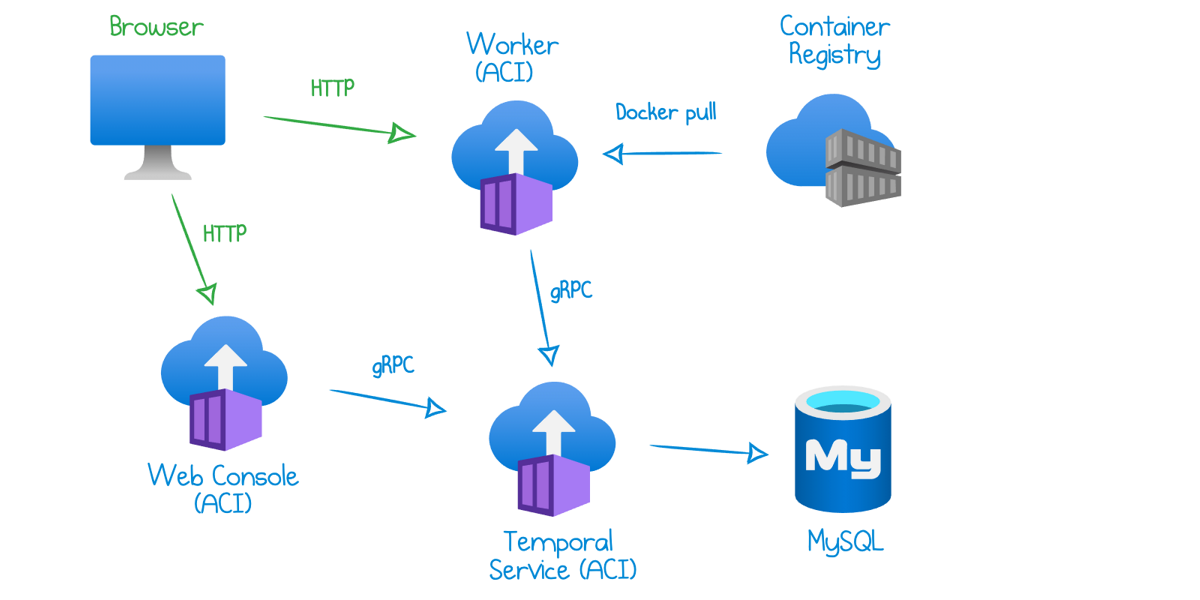
Read more...
How To Deploy Temporal to Azure Container Instances
Get up and running with Temporal workflows in Azure in several CLI commands
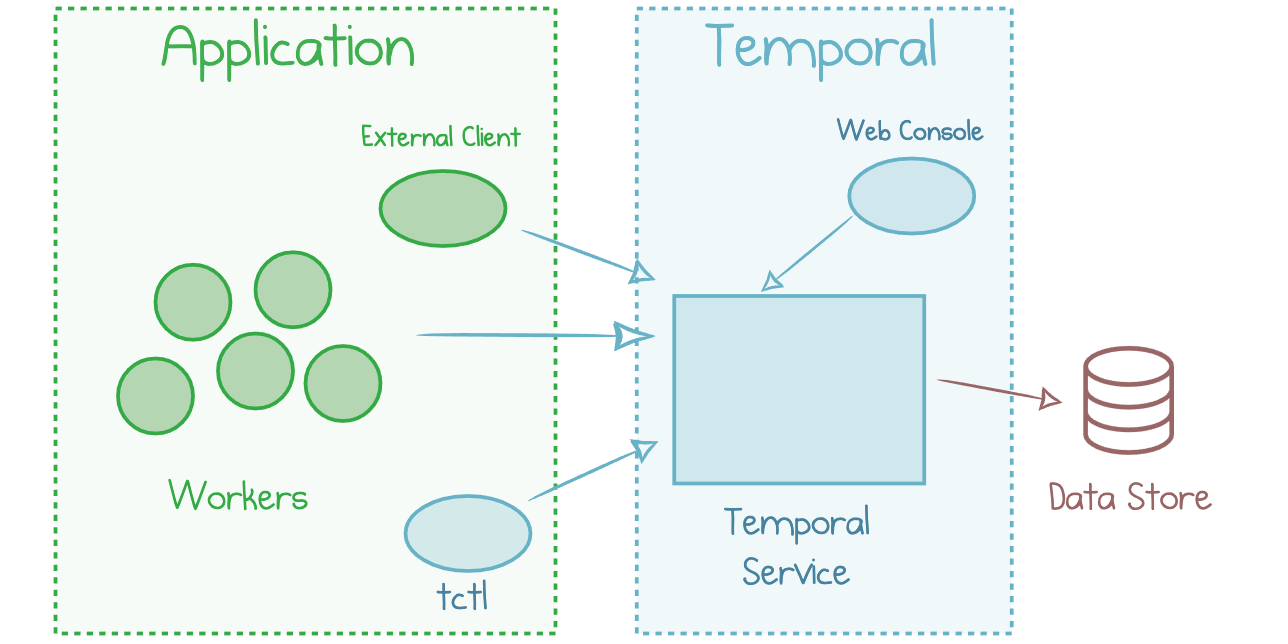
Read more...
A Practical Approach to Temporal Architecture
What it takes to get Temporal workflows up and running
Read more...
Temporal: Open Source Workflows as Code
Temporal reimagines state-dependent service-orchestrated application development
Read more...
Announcing Next Generation Pulumi Azure Provider
Next Generation Pulumi Azure Provider with 100% API Coverage and Same-Day Feature Support is now available in beta
Read more...
How to Drain a List of .NET Tasks to Completion
Custom await logic for a dynamic list of .NET tasks, fast and on-time
Read more...
The Emerging Landscape of Edge-Computing
What is edge computing, and what are the primary use cases in the world today? (a paper review)
Read more...
The Best Interview is No Interview: How I Get Jobs Without Applying
My humble story of getting (or not) a job at Amazon, Qualcomm, Jet.com, Pulumi, and more
Read more...
Eliminate Cold Starts by Predicting Invocations of Serverless Functions
Azure Functions introduce a data-driven strategy to pre-warm serverless applications right before the next request comes in
Read more...
Serverless in the Wild: Azure Functions Production Usage Statistics
Insightful statistics about the actual production usage of Azure Functions, based on the data from Microsoft's paper
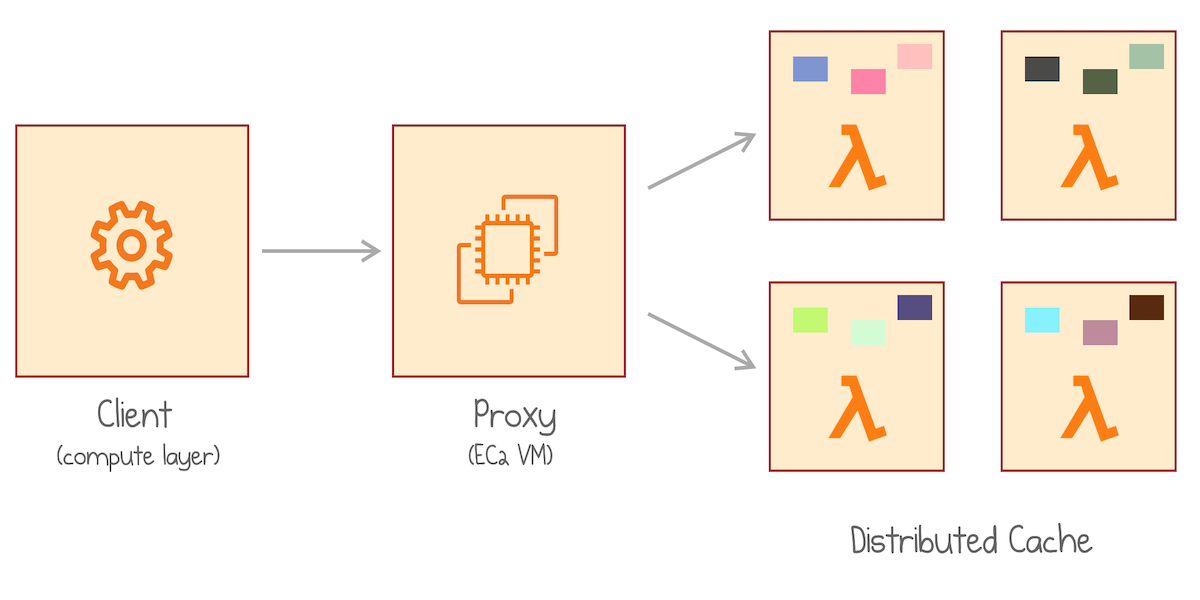
Read more...
InfiniCache: Distributed Cache on Top of AWS Lambda (paper review)
My review of the paper "InfiniCache: Exploiting Ephemeral Serverless Functions to Build a Cost-Effective Memory Cache"
Read more...
Hosting Azure Functions in Google Cloud Run
Running Azure Functions Docker container inside Google Cloud Run managed service
Read more...
Serverless Containers with Google Cloud Run
Google Cloud Run is the latest addition to the serverless compute family. While it may look similar to existing services of public cloud, the feature set makes Cloud Run unique.
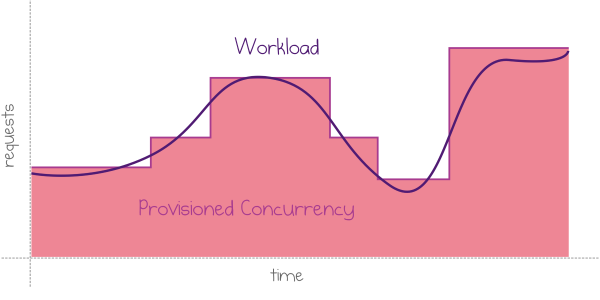
Read more...
Provisioned Concurrency: Avoiding Cold Starts in AWS Lambda
AWS recently announced the launch of Provisioned Concurrency, a new feature of AWS Lambda that intends to solve the problem of cold starts.
Read more...
Santa Brings Cloud to Every Developer
How Santa Cloud uses F# and Pulumi to bring cloud resources to the homes of software engineers.
Read more...
Choosing the Best Deployment Tool for Your Serverless Applications
Factors to consider while deploying cloud infrastructure for serverless apps.
Read more...
AWS Lambda vs. Azure Functions: 10 Major Differences
A comparison AWS Lambda with Azure Functions, focusing on their unique features and limitations.
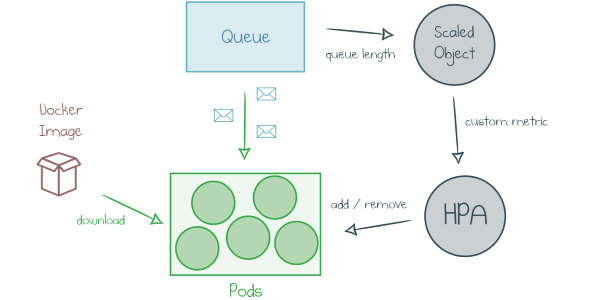
Read more...
How To Deploy a Function App with KEDA (Kubernetes-based Event-Driven Autoscaling)
Hosting Azure Functions in Kubernetes: how it works and the simplest way to get started.
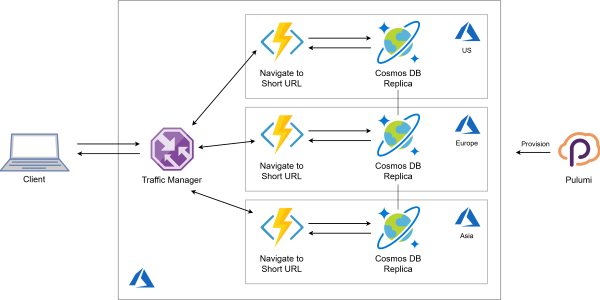
Read more...
How To Build Globally Distributed Applications with Azure Cosmos DB and Pulumi
A reusable component to build highly-available, low-latency applications on Azure
Read more...
How to Avoid Cost Pitfalls by Monitoring APIs in AWS Lambda
How to monitor your APIs using serverless technologies and an Epsagon dashboard.
Read more...
Ten Pearls With Azure Functions in Pulumi
Ten bite-sized code snippets that use Pulumi to build serverless applications with Azure Functions and infrastructure as code.
Read more...
How to Measure the Cost of Azure Functions
Azure pricing can be complicated—to get the most value out of your cloud platform, you need to know how to track spend and measure the costs incurred by Azure Functions.
Read more...
7 Ways to Deal with Application Secrets in Azure
From config files to Key Vault and role-based access, learn how infrastructure as code helps manage application secrets in Azure.
Read more...
Load-Testing Azure Functions with Loader.io
Verifying your Function App as a valid target for the cloud load testing.
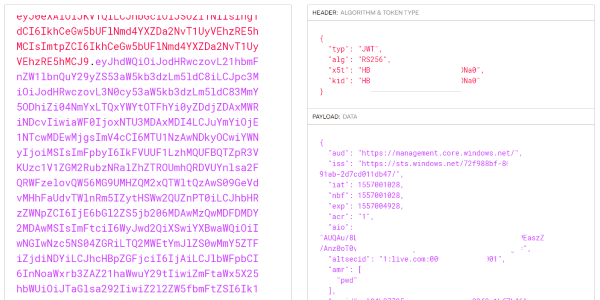
Read more...
How Azure CLI Manages Your Access Tokens
Azure CLI is a powerful tool to manage your cloud resources. Where does it store the sensitive information and why might you want to care?
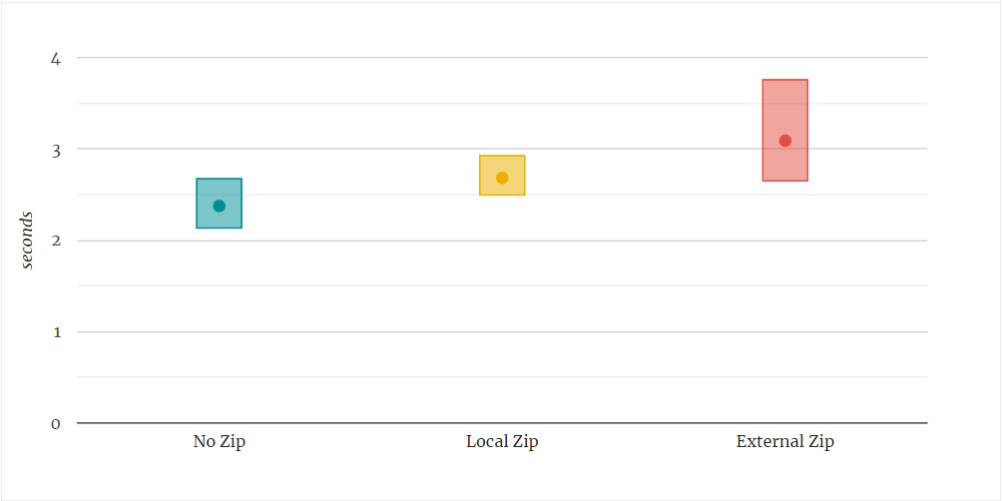
Read more...
Globally-distributed Serverless Application in 100 Lines of Code. Infrastructure Included!
Building a serverless application on Azure with both the data store and the HTTP endpoint located close to end users for fast response time.
Read more...
Concurrency and Isolation in Serverless Functions
Exploring approaches to sharing or isolating resources between multiple executions of the same cloud function and the associated trade-offs.
Read more...
Reducing Cold Start Duration in Azure Functions
The influence of the deployment method, application insights, and more on Azure Functions cold starts.
Read more...
From YAML to TypeScript: Developer's View on Cloud Automation
An expressive and powerful way to design cloud-native and serverless infrastructure
Read more...
Serverless at Scale: Serving StackOverflow-like Traffic
Scalability test for HTTP-triggered serverless functions across AWS, Azure and GCP
Read more...
A Fairy Tale of F# and Durable Functions
How F# and Azure Durable Functions make children happy (most developers are still kids at heart)
Read more...
Making Sense of Azure Durable Functions
Why and How of Stateful Workflows on top of serverless functions
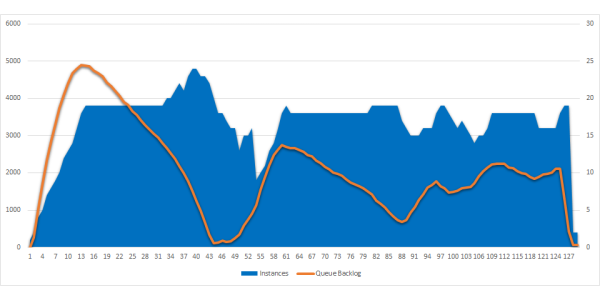
Read more...
From 0 to 1000 Instances: How Serverless Providers Scale Queue Processing
Comparison of queue processing scalability for FaaS across AWS, Azure and GCP
Read more...
Monads explained in C# (again)
Yet another Monad tutorial, this time for C# OOP developers
Read more...
Cold Starts Beyond First Request in Azure Functions
Can we avoid cold starts by keeping Functions warm, and will cold starts occur on scale out? Let's try!
Read more...
Load Testing Azure SQL Database by Copying Traffic from Production SQL Server
Azure SQL Database is a managed service that provides low-maintenance SQL Server instances in the cloud. You don’t have to run and update VMs, or even take backups and setup failover clusters.
Read more...
Tic-Tac-Toe with F#, Azure Functions, HATEOAS and Property-Based Testing
A toy application built with F# and Azure Functions: a simple end-to-end implementation from domain design to property-based tests.
Read more...
Azure Functions Get More Scalable and Elastic
Back in August this year, I’ve posted Azure Functions: Are They Really Infinitely Scalable and Elastic? with two experiments about Azure Function App auto scaling. I ran a simple CPU-bound function based on Bcrypt hashing, and measured how well Azure was running my Function under load.
Read more...
Precompiled Azure Functions in F#
This post is giving a start to F# Advent Calendar in English 2017. Please follow the calendar for all the great posts to come. Azure Functions is a “serverless” cloud offering from Microsoft.
Read more...
Authoring a Custom Binding for Azure Functions
The process of creating a custom binding for Azure Functions.
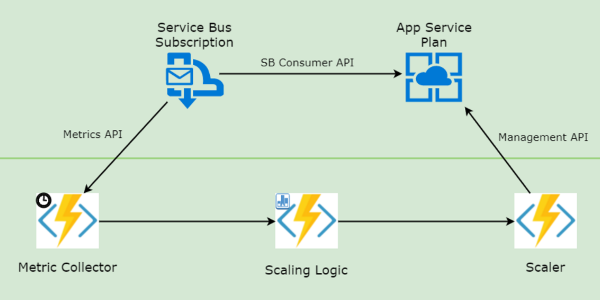
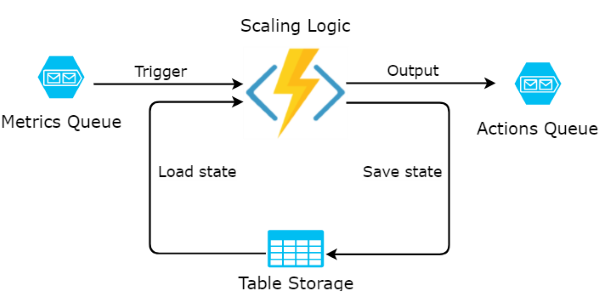
Read more...
Custom Autoscaling with Durable Functions
Leverage Azure Durable Functions to scale-out and scale-in App Service based on a custom metric
Read more...
Custom Autoscaling of Azure App Service with a Function App
How to scale-out and scale-in App Service based on a custom metric
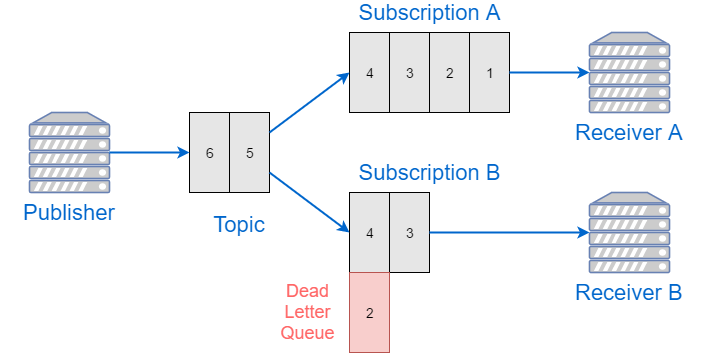
Read more...
Sending Large Batches to Azure Service Bus
Azure Service Bus client supports sending messages in batches. However, the size of a single batch must stay below 256k bytes, otherwise the whole batch will get rejected.
Read more...
Finding Lost Events in Azure Application Insights
One of the ways we use Azure Application Insights is tracking custom application-specific events. For instance, every time a data point from an IoT device comes in, we log an AppInsights event.
Read more...
Reliable Consumer of Azure Event Hubs
Azure Event Hubs is a log-based messaging system-as-a-service in Azure cloud. It’s designed to be able to handle huge amount of data, and naturally supports multiple consumers.
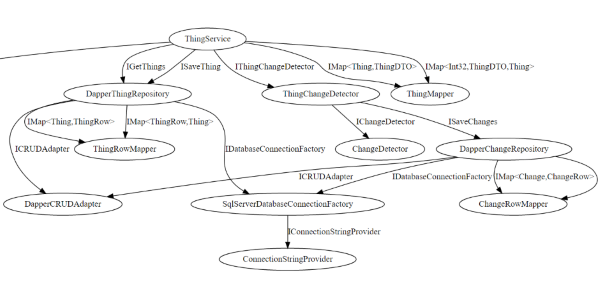
Read more...
Visualizing Dependency Tree from DI Container
So you are a C# developer. And you need to read the code and understand its structure. Maybe you’ve just joined the project, or it’s your own code you wrote 1 year ago.
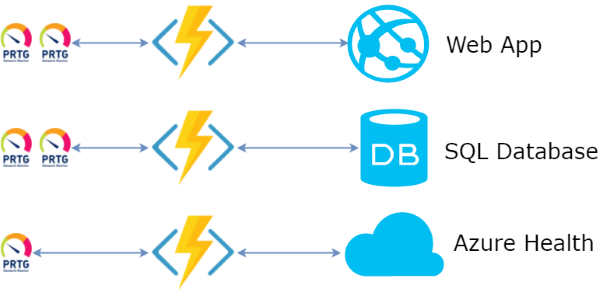
Read more...
Azure Functions as a Facade for Azure Monitoring
Azure Functions are the Function-as-a-Service offering from Microsoft Azure cloud. Basically, an Azure Function is a piece of code which gets executed by Azure every time an event of some kind happens.
Read more...
Coding Puzzle in F#: Find the Number of Islands
Here’s a programming puzzle. Given 2D matrix of 0’s and 1’s, find the number of islands. A group of connected 1’s forms an island. For example, the below matrix contains 5 islands
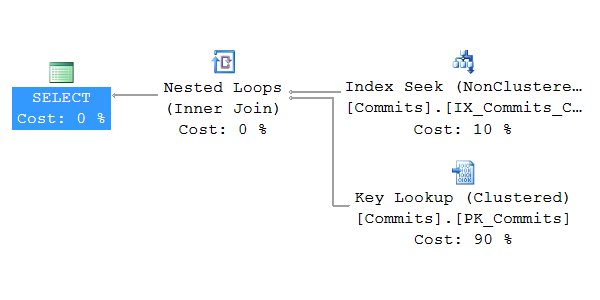
Read more...
Event Sourcing: Optimizing NEventStore SQL read performance
In my previous post about Event Store read complexity I described how the growth of reads from the event database might be quadratic in respect to amount of events per aggregate.
Read more...
My Praise of Advent of Code 2016
During the last days of December I was pleasing my internal need for solving puzzles and tricky tasks by going through Advent of Code 2016 challenge.
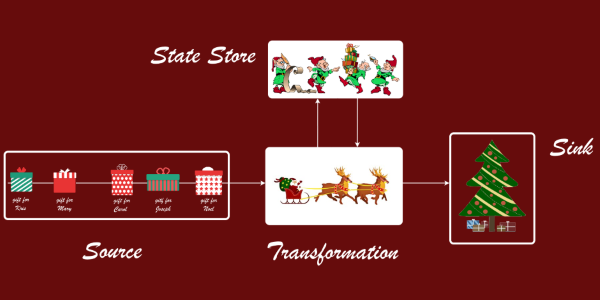
Read more...
Introducing Stream Processing in F#
The post was published for F# Advent Calendar 2016, thus the examples are themed around the Christmas gifts. This article is my naive introduction to the data processing discipline called Stream Processing.
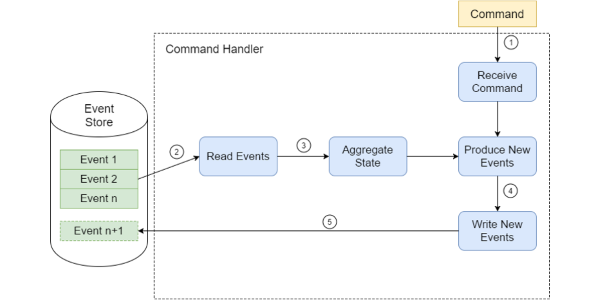
Read more...
Event Sourcing and IO Complexity
Event Sourcing is an approach, when an append-only store is used to record the full series of events that describe actions taken on a particular domain entity.
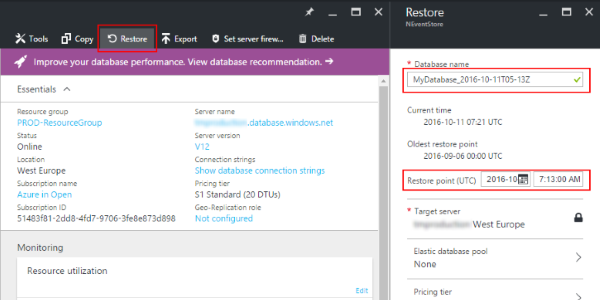
Read more...
Azure SQL Databases: Backups, Disaster Recovery, Import and Export
Azure SQL Database is a managed cloud database-as-a-service. It provides application developers with SQL Server databases which are hosted in the cloud and fully managed by Microsoft.
Read more...
Comparing Scala to F#
F# and Scala are quite similar languages from 10.000 feet view. Both are functional-first languages developed for the virtual machines where imperative languages dominate. C# for .NET and Java for JVM are still lingua franca, but alternatives are getting stronger.
Read more...
Building a Poker Bot: Functional Fold as Decision Tree Pattern
This is the fifth part of Building a Poker Bot series where I describe my experience developing bot software to play in online poker rooms. I’m building the bot with .
Read more...
Dependency Inversion Implies Interfaces Are Owned by High-level Modules
Dependency Inversion is one of the five principles of widely known and acknowledged S.O.L.I.D. design guidelines. This principle is very powerful and useful when applied consistently.
Read more...
Building a Poker Bot with Akka.NET Actors
This post lays out the most exciting part of the bot. I'll compose the recognition, flow, decision and mouse clicking parts together into the bot application. The application is a console executable interacting with multiple windows of poker room software.
Read more...
Functional Actor Patterns with Akka.NET and F#
My exploration of Actor model started with Akka.NET framework - a .NET port of JVM-based Akka. Actor programming model made a lot of sense to me, but once I started playing with it, some questions arose.
Read more...
Building a Poker Bot: Mouse Movements
The last step of the poker bot flow: clicking the buttons. The screen is already recognized, the hand is understood, the decisions are made and now the bot needs to execute the actions. This means clicking the right button at the poker table.
Read more...